Convert Megapascal (MPa) to Pound Per Square Inch (psi)
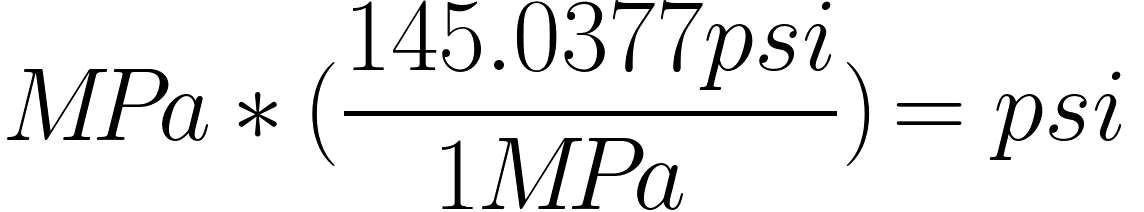
MPa to psi conversion equation
Above: MPa to psi conversion equation and formula
Convert Pound Per Square Inch (psi) to Megapascal (MPa)
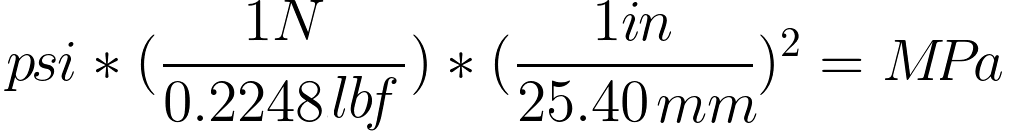
psi to MPa conversion equation
Above: psi to MPa conversion equation and formula
Converting psi to MPa is a common task when designing metal tube applications. With that in mind, a major concern with metal tubing is its ability to withstand pressures, both external and internal. Additionally, the forces of atmospheric pressure and vacuum are factors when calculating the pressure a tube can withstand.

Psi MPa Pressure Gauges
The pressure that steel tube can withstand matters in determining its efficiency, safety, and reliable use. Both psi and MPa measure pressure within a metal tube. For this reason, we provide psi MPa Converter tools below.
Psi Versus Megapascal
First, both are a measure of internal pressure. However, psi is an imperial unit measurement while MPa is metric as part of SI units (International System of Units abbreviated from the French Système international).
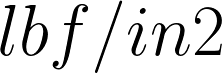
psi equation
Pressure Measurement using psi, psia, and psig
Simply put, psi or Pound-Force Per Square Inch is the measure of force in pounds exerted onto an area of one square inch. On the other hand, psia stands for psi as an absolute pressure measured relative to a complete vacuum. On the other hand, Psig considers pressure (psi) relative to atmospheric pressure (e.g. atmospheric pressure at sea level is approximately 14.7 psi).
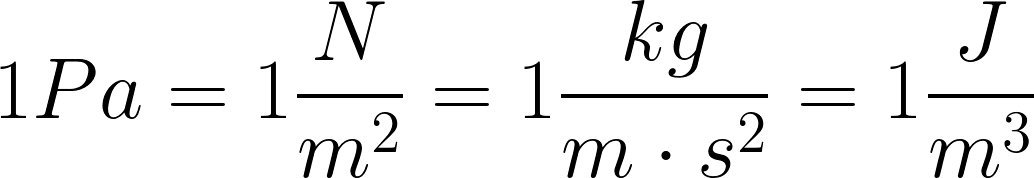
Pascal equation
MPa, kPa, and Pa

Painting of Blaise Pascal Versailles, French mathematician inventor of the Pascal.
Similarly, MPa and other measurements ending in Pa are pressure units much like psi. A Pascal, whose symbol Pa was the brainchild of Blaise Pascal, a French polymath of the 16th Century. As a result of Pascal’s many talents (e.g. Mathematician, Physicist, Poet, Inventor, and religious Philosopher), he inspired the modern-day
Theory of Probabilities. Because of Blaise’s “Pascal’s law” or “Pascal’s principle“, MPa is as ubiquitous in Europe as psi is in the United States. As an example, the aeronautics industry uses Pascal’s Principle and Hydraulics to engineer and design hydraulic systems.
Pascal’s law states that when there is an increase in pressure at any point in a confined fluid, there is an equal increase at every other point in the container. **
References
** Hodanbosi, C. and Fairman, J. (1996). Pascal’s Principle and Hydraulics. [online] Grc.nasa.gov. Available at: https://www.grc.nasa.gov/www/k-12/WindTunnel/Activities/Pascals_principle.html [Accessed 25 Apr. 2019].
